by Steven K. Roberts
Columbus, Ohio 
August, 1981

I have recently found myself spending a lot of time at AI conferences in journalist mode, and have become particularly enamored with image recognition. This fledgling pursuit has been sufficiently captivating to propel me into the study of human vision, and I have been fortunate to spend time with many of the luminaries in the field (including a few months working in VER research, developing bar & checkerboard stimulus generators for presenting image changes on the retina with no net luminance change, studying the layers of feature abstraction implemented in the brain, and reviewing texts on the subject then spending time with their authors).

In the midst of all this, I came across an intriguing paper from the NYU Medical Center, reporting the sectioning and TEM (transmission electron-microscopy) of the entire visual pathway from retina to primary visual cortex. In the paper was an understated but startling observation: there is a coordinate transformation from a logarithmic polar system (at the retina) to a cartesian system (at the cortex), implemented entirely in the hardwiring of the optic nerve. This struck me as rather bizarre, and I assumed that it created a sensor density gradient biased to the macular region, while supporting our column-interleaved focusing system. But still it nagged at me, and not being much of a mathematician I didn’t grasp the significance.

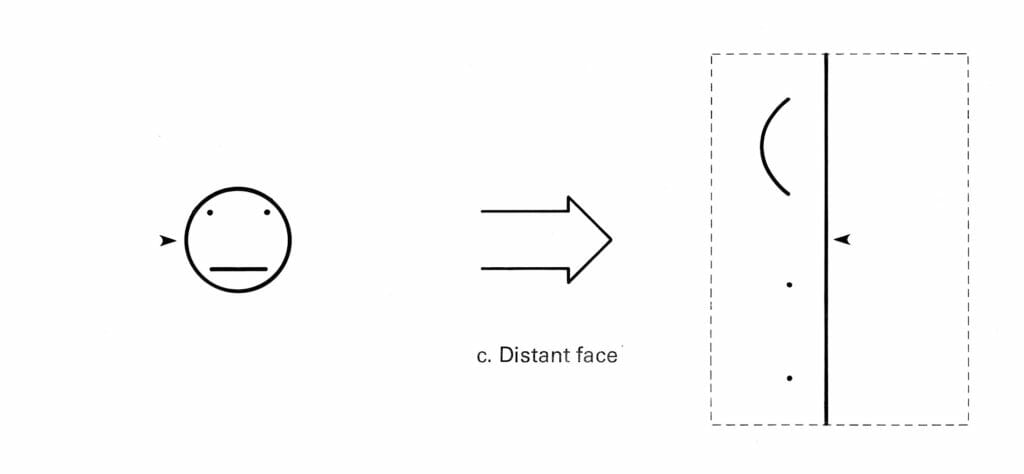
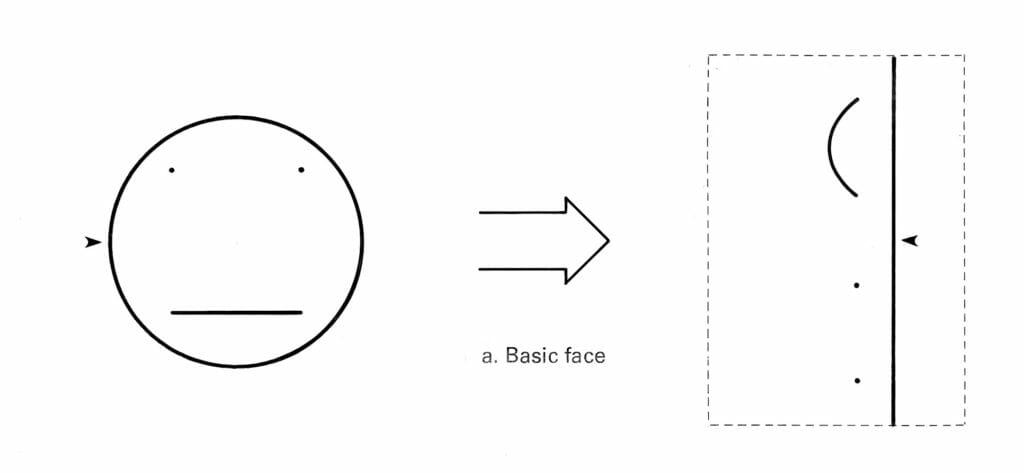
Finally, out of curiosity, I wrote a coordinate transformation program on my Cromemco Z-2D system, and presented it with a simple “face” graphic to see what happened. This is shown here (the arrow is just a reference point, for reasons that will become clear in a moment). Output was printed by a Diablo daisy-wheel printer in micro-stepping mode.

As you can see, the circle, being a constant distance from the origin, becomes a vertical line. The eye dots are uninteresting, since they are just dots. And the mouth line (my drawing tools are no more sophisticated than my artistic ability) becomes a little logarithmic curve. That last bit is interesting, and I stared at it a while, wondering what I had done wrong.

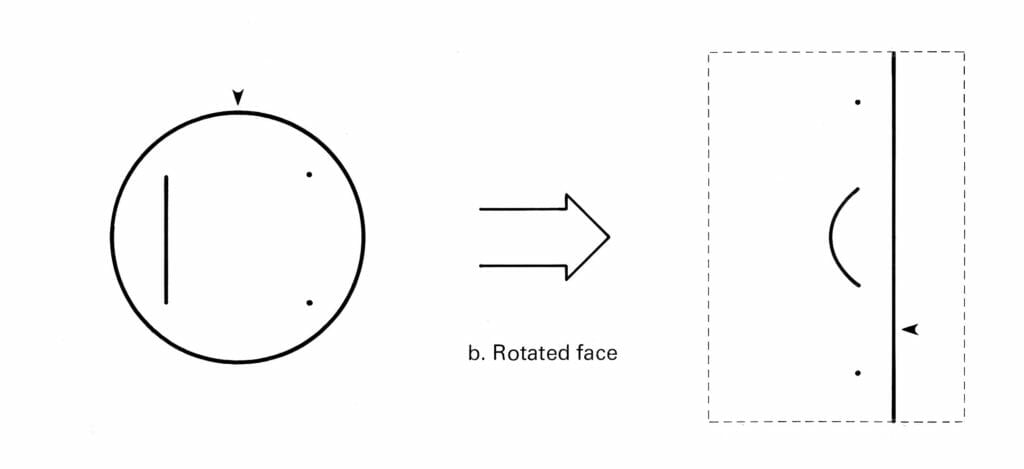
To aid in debugging, I rotated the input image and almost fell off my chair. The output is identical, merely translated vertically (wrapping around my memory-mapped display space; hence the added arrow for reference):

With growing excitement, I tried scaling the input image, and the result is just as shocking… again, the output is identical, merely translated horizontally.

What we see here is an elegant and simple solution to a complex problem… dealing with rotation and scaling when attempting to perform image recognition. The hardwired mapping from logarithmic polar grid to a rectangular cartesian system converts the rotation of an object we see in real space into a vertical translation, and expansion or contraction is converted into a horizontal translation. In other words, tilting of the “face” (or its approach or recession) produces no net pattern change of the image presented to the brain.

(Note that real-world lateral translation would create distortion through this mapping, but we deal with that by automatically directing our receptors and visual attention to the subject under analysis, effectively centering it.)

This would appear to solve one of the most difficult problems in computer image recognition, replacing it with the much simpler challenge of keeping the object of interest centered in the frame of reference (presumably using centrums and other context-aware tricks).

If we are trying to do this in a computer, the template faces would all be stored as pre-transformed images, and the input subjected to the same treatment (conceivably with a passive fiber-optic device; there is no reason it has to be computational, though that may be easier). Spatial FFT-based correlation would then have a much less difficult time dealing with rotation and scaling, at least within a 2-D space (this won’t help at all with pitch and yaw distortions). Obviously there’s a lot more to image recognition than simple coordinate transformation and cross-correlation, but I’m reasonably convinced that this should be investigated as a preprocessing step… it’s how we have evolved to solve the identical problem.

2019 Commentary

This text has been sitting around my life for decades, and the images were used in my engineering textbook, Industrial Design with Microcomputers (Prentice-Hall, 1982). Naturally, we have come a long way in nearly four decades, and I’m sure that real investigators in this field have long since incorporated this, or found alternative explanations that go far beyond my own primitive observations.

Still, I include this in the archive as a demonstration of the power of cross-pollination… interesting stuff happens at the boundaries between specialties, and seeding primitive computer image recognition with insights from electron microscopy of the retina and optic nerve is one of my favorite examples. 

Chapters 25-28 of the Kandel book discuss this system in far greater detail, though without specifically mentioning this mapping (which is predicated on that NYU paper and may not reflect current understanding):

This is an example of what can happen when a curious newbie like me reads something, doesn’t understand its implications, then constructs an experiment to make sense of the data. I had a longer attention span back then; if that happened today, I’d Google it to yield a paper or two about retinotopy, marvel for a few minutes, then shrug and get back to browsing Facebook. I remember the obsessive quest that evening long ago, the delighted sense of absolute shock when I realized what was happening, and the frustration of not knowing how to productize it… especially when I realized that it could profoundly change the field of image recognition. 

Posted in Articles by SKR and tagged